While “problem-solving” may seem to be an abstract concept, in Mathematics education it has a more specific definition. In the new, linear mathematics A-Level, students are required to “recognise the underlying mathematical structure in a situation and simplify and abstract appropriately to enable problems to be solved.”[1] Depending on your experience, this may be a very clear definition or a very nebulous one, but this is essentially referring to situations where students need to select the right approach to answer a question, where this may not be immediately obvious from the stimulus given in the question. As part of developing the research-based teaching and learning culture at CATS Cambridge, in line with the CamSTAR teacher research programme, this article explores some of the ways I have researched of best developing problem-solving ability in students.
As teachers, it is often tempting to “teach problem-solving” by demonstrating solutions to questions which involve this process. This process is often seen in lessons:
- Discuss which skills (areas of Maths) will be needed based on the information available in the question.
- Discuss a strategy: What information do we have? What is needed to be found to solve this problem?
- Demonstrate the solution.
However, while this may give students an instant dopamine hit of understanding how you have solved this problem, there is little to suggest that they will be able to apply the ideas demonstrated to a new situation.
For example, consider the following chess puzzle:

White to play and win[2]
Since chess and Maths are both inherently logic and reasoning-based disciplines, it seems appropriate to use one as a proxy for the other (note that you do not need to know about chess to engage with the rest of this article!).
For the puzzle above, as the teacher I could explain the various moves available to white, talk about the fact that black’s safety is dependent on the ability to run the king away to d7, and then talk through the series of moves needed to win the game. You may then think “excellent, if this position comes up in a game, I know what to do!”. But would you? Also, more importantly, would you then be able to apply this reasoning to a new situation, say for example this puzzle:

White to play and win[3]
At this point your confidence in your ability may be waning, as you cannot instinctively appreciate that these two puzzles have the same underlying structure in common. While I might believe I have “taught” you how to solve this problem by showing you the last example, you may find yourself no more able to proceed here than if you were coming into this problem fresh. This is the trap we can easily fall into as teachers of mathematics, as we can confuse understanding of a solution with a development in problem-solving ability.
The research on this suggests that it is actually very difficult to develop students’ problem-solving ability. In “Analogical problem solving”, Glick and Holyoak (1980)[4] demonstrated that participants given two problems with the same deep structure, but different surface structure, one after the other, the vast majority of participants failed to spot the connections due to distractions in the surface structure. This is something which you as the reader may have experienced yourself with the chess puzzles above; the two puzzles share a common theme, but it may not be obvious given the different arrangement of the pieces.
In 1957, George Pólya suggested in “How to Solve it”[5], that good problem-solving involves these four steps:
- Understand the problem
- Make a plan
- Carry out the plan
- Look back on your work.
This is what students need to be able to do, but can this process be taught? Also, can the processes be taught independently of each other?
The first step is easy for “experts”, as one definition of a subject specialist is the ability to recognise the deep structure of a problem and overcome potential surface distractions. A chess grandmaster should be able to solve these problems as they will inherently recognise the key composition of the two problems from the many, many games they will have played over their career. I am always reminded of the Herbert Simon quote “Intuition is nothing more and nothing less than recognition” in situations such as these, but intuition independent of experience is hard to teach.
Similarly, in steps two and three Pólya suggests a few general problem-solving strategies (including the very optimistic “be ingenious”), however in “Problem-Solving Strategies: Research Findings from Mathematics Olympiads”, Pak-Hong (2012)[6] in a follow on from Pólya’s work, concluded that “… while heuristics suggested by Pólya are useful in analysing the problems and in exploring feasible solutions, most of the more effective strategies are topic oriented.” So, research suggests that using mathematical specific strategies will be more effective than more general, abstract ideas which could apply to a multitude of subjects. Of course, this must be built on the assumption that the requisite domain-specific knowledge is there in the first place; you cannot solve the puzzles above if you cannot play chess. But topic-oriented strategies can be too narrow, and the skills learned here may not transfer to other areas effectively. This point is supported by Herbert Simon and William Chase, who in their famous study “Perception in Chess”[7] concluded that while chess grandmasters had a greatly above average speed of recalling ‘normal’ chess positions after only five seconds of viewing, this dropped to an average performance when the pieces were placed randomly on the board. One conclusion of this is that domain-specific strategies may not be easily transferrable to other areas. The strategies employed by the grandmasters were clearly effective when the pieces were arranged in a familiar structure, but not effective for when the pieces were located randomly.
However, in addition to generic and topic-specific strategies, there is also a meta-cognitive approach. Shoenfeld (various works) argues that expert problem solvers frequently engaged in meta-cognitive acts in which they reflect on the approaches they are using. They ask questions such as “is this approach going anywhere?”, or “Is there another way I can represent this problem?”. In “Learning to think Mathematically: Problem-Solving, Metacognition, and Sense-Making in Mathematics”[8], Shoenfeld writes “For the most part, students are unaware of or fail to use the executive skills demonstrated by the expert. However, it is the case that such skills can be learned as a result of explicit instruction that focuses on metacognitive aspects of mathematical thinking. That instruction takes the form of “coaching,” with active interventions as students work on problems”
Shoenfeld’s work is based on the research of Lester et al. (1989) in “The Role of Metacognition in Mathematical Problem Solving”[9]. Here, the researchers attempt “to determine the influence of metacognition on the cognitive processes students use during mathematical problem solving” as one of two goals in this paper.
The authors conclude: “In general, it seems that the more successful problem solvers in our study were better able to monitor and regulate their problem-solving activity than the poorer problem solvers, with the difference being most apparent during the orientation phase. …the good problem solvers tended to be concerned with developing a meaningful sense about the conditions and questions in problems, whereas the weaker problem solvers tended to be content with superficial understanding. That is, the good problem solvers were concerned about structural features of problems, while poor problem solvers focused on surface level features of problems.” While problem solving skills can be challenging to directly develop, meta-cognitive abilities can be strengthened. At the time, it was not known if a strong meta-cognitive approach and problem-solving ability were causally linked, however Shoenfeld concluded they were.
The Education Endowment Foundation states that “…evidence suggests the use of ‘metacognitive strategies’ – which get pupils to think about their own learning – can be worth the equivalent of an additional +7 months progress when used well.”, which is strong evidence that this is worth pursuing[10]. So how can metacognition be developed in students? One suggested model in “Learning to think Mathematically” breaks the process down into actions before the problem begins, during it and after it:
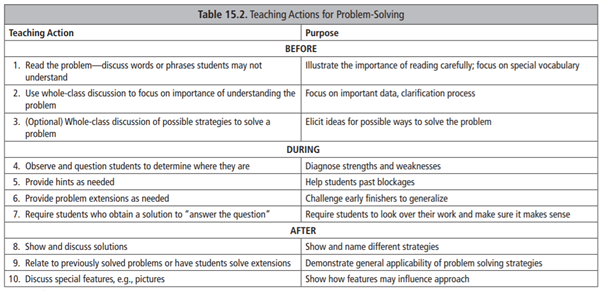
In the “during” phase of the above, it was suggested it is useful to ask questions which engender a metacognitive thought process. For example, students could be asked:
- “What exactly are you doing here?”
- “Why are you doing this?”
- “How does this approach help you?”
These are questions specifically designed to get students to reflect on their thought processes.
Development of metacognitive ability is not something which will happening instantaneously. Problem-solving can be demonstrated, however demonstrating a problem-solving process does not mean development in problem-solving ability. This investigation into problem-solving ability has helped me to see this aspect of mathematics education differently and begin to change the philosophy of my department to better reflect the pedagogical theory surrounding this. In the Maths department at CATS Cambridge, we are now overtly attempting to instil a metacognitive approach in students’ learning through adapting our teaching in line with the suggestions above. So far, students have been receptive to this approach and are appreciative of the fact staff are following research-based approaches when planning and delivering their lessons.
By slowly developing a culture where students approach problems in this way, research suggests that we can make them better problem-solvers, and maybe also better chess players too. I look forward to seeing the effects of this initiative as the academic year progresses.
Rob Mathers
Head of Mathematics
Many of the ideas in this article are referenced in Chapter 9 of the book “How I Wish I’d Taught Maths” by Craig Barton.[11]
[1] From https://qualifications.pearson.com/content/dam/pdf/A%20Level/Mathematics/2017/specification-and-sample-assesment/a-level-l3-mathematics-specification-issue4.pdf
[2] From Luis Paulo Supi vs Magnus Carlsen (2020).
[3] From Magnus Carlsen vs Sergey Karjakin (2016)
[4] Gick, M. L., & Holyoak, K. J. (1980). Analogical problem solving. Cognitive Psychology, 12(3), 306–355.
[5] Pólya, G., Pólya, G. (1971). How to solve it: a new aspect of mathematical method. United Kingdom: Princeton University Press.
[6] Pak-Hong, C. (n.d.). Problem-Solving Strategies: Research Findings from Mathematics Olympiads. 20.
[7] Chase, W. G., & Simon, H. A. (1973). Perception in chess. Cognitive Psychology, 4(1), 55–81. https://doi.org/10.1016/0010-0285(73)90004-2
[8] Schoenfeld, A. H. (n.d.). LEARNING TO THINK MATHEMATICALLY: PROBLEM SOLVING, METACOGNITION, AND SENSE-MAKING IN MATHEMATICS. 102.
[9] Lester, F. K., & And Others. (1989). The Role of Metacognition in Mathematical Problem Solving: A Study of Two Grade Seven Classes. Final Report.
[10] From https://educationendowmentfoundation.org.uk/education-evidence/guidance-reports/metacognition
[11] “How I Wish I’d Taught Maths” by Craig Barton.




